2021年1月29日，北京量子信息科学研究院兼聘研究员、清华大学教授龙桂鲁领导的团队在Nature子刊《量子信息期刊》上发表文章指出，将之前的量子梯度下降算法做进一步改进提升，可以降低先前算法对量子线路的资源需求，使得能够采用现有的量子系统运行该算法。预计在高维数据优化问题上，该量子算法将能够体现出超过经典算法的优势。

梯度下降法是传统数值最优化计算的核心之一，也是当前众多机器学习算法的重要部分。梯度下降算法的中心思想是通过不断迭代使目标函数沿着最优梯度方向演化，从而找到目标函数的局部最小值。然而，在高维数据的最优化问题中，实现这种优化将消耗大量的计算资源，甚至可能以目前的经典计算能力难以解决。为了解决这个问题，有研究人员结合量子计算的优势，提出了量子版本的梯度下降算法，该量子算法采用了量子相位估计方法，因而需要深度较大的量子线路，以当前的量子门操作误差等因素难以实现。

龙桂鲁教授团队提出的改进版本算法，即利用龙桂鲁提出的酉算子线性组合(LCU)方法，发展了量子梯度算法，给出了量子线路表示，将量子态拷贝数量从多项式数目减少为与系统大小无关的常数2，大幅度降低了线路的深度，使其量子门操作数目大幅减少，可在当前资源有限的量子处理器上实现。该团队在一个4比特的核磁共振体系中演示了该改进后的算法，实现多项式问题的优化。其以1个量子比特状态构成的二维矢量作为待优化问题，在多种给定初始值条件下演示了该算法，实验获得局部最小值的保真度大于94%。

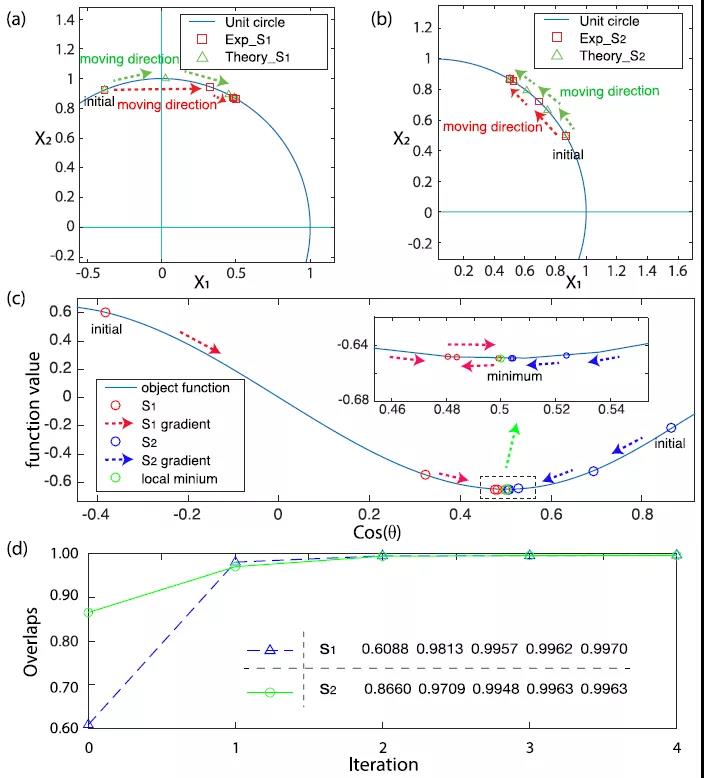
如图所示，从不同的初始点出发，量子梯度算法都可成功寻找到极值。这一算法可直接用于大数据分析中的多维比例缩放问题。图(a)、(b)和(c)展示了不同初始点收敛到极值点的过程。其中绿色和红色分别代表理论模拟和实验实现。(d)描述了实验上每一步梯度迭代中量子态的保真度。

随着量子计算机硬件的发展，这一量子梯度下降算法显示出在相关领域潜在的重要应用价值。这项工作可为高维优化问题提供更快的解决方案。特别是，和团队之前采用LCU方法构造的全量子本征求解算法一样，不仅可在现在的含噪声量子计算装置上运行，而且可作为一个应用程序软件直接在未来的可容错量子计算机上使用。

论文信息：https://doi.org/10.1038/s41534-020-00351-5

2021-02-08