梯度下降法是传统数值最优化计算的核心之一，也是当前众多机器学习算法的重要部分。梯度下降算法的中心思想是通过不断迭代使目标函数沿着最优梯度方向演化，从而找到目标函数的局部最小值。然而，在高维数据的最优化问题中，实现这种优化将消耗大量的计算资源，甚至可能用以目前的经典计算能力难以解决。为了解决这个问题，有研究人员结合量子计算的优势，提出了量子版本的梯度下降算法，但该量子算法仍然难以采用现有规模的量子系统实现。

近日，国内的龙桂鲁教授研究团队将之前的量子梯度下降算法做了进一步改进提升，并提出了如何在实际量子系统中实现该算法。之前版本的量子梯度下降算法采用了量子相位估计方法，因而需要深度较大的量子线路，以当前的量子门操作误差等因素难以实现。而该团队提出的改进版本算法，则是采用幺正操作的线性组合来实现，大大降低了对量子线路的资源需求，并且只需要待优化量子态（即待优化问题）的两份拷贝，从而能够在现有的量子系统中实现。该团队在一个4比特的核磁共振体系中演示了该改进后的算法，实现多项式问题的优化。其以一个量子比特状态构成的二维矢量作为待优化问题，在多种给定初始值条件下演示了该算法，实验获得局部最小值的保真度大于94%。

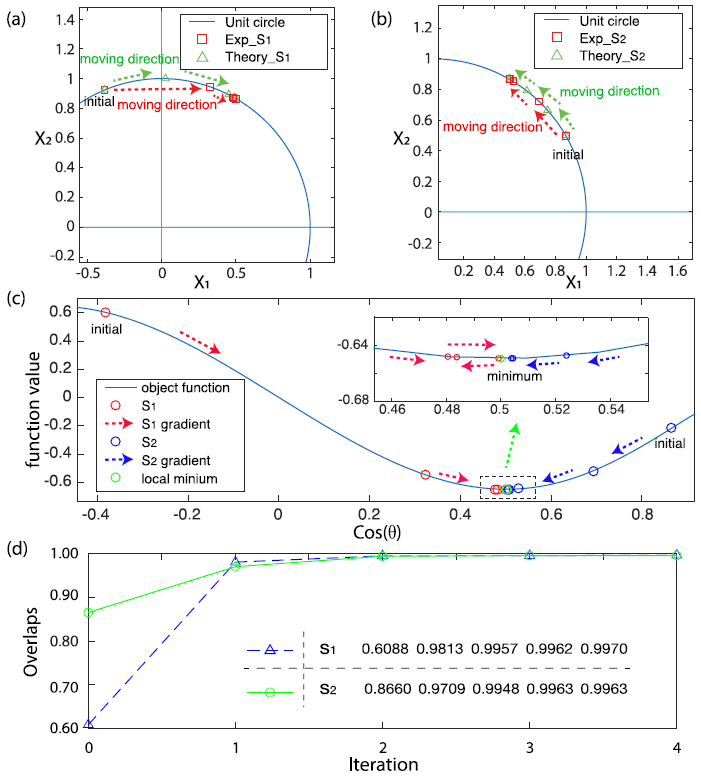
这种改进的量子梯度下降算法降低了先前算法对量子线路的资源需求，使得能够采用现有的量子系统运行该算法，预计在高维数据优化问题上，该量子算法将能够体现出超过经典算法的优势。

论文信息：https://doi.org/10.1038/s41534-020-00351-5